什么是勾股定理-勾股定理的定义

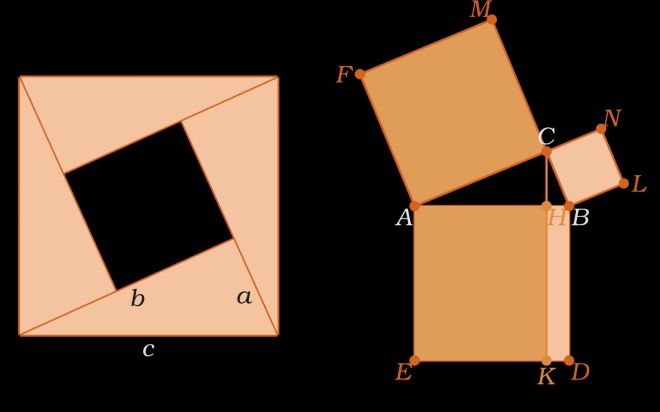
勾股定理又叫做“毕达哥拉斯定理”，是数学中的一个重要定理，它描述了直角三角形中三边之间的关系。勾股定理的定义是：在一个直角三角形中，直角边的平方和等于斜边的平方。

具体来说，在一个直角三角形ABC中，设边AB为直角边，边AC和边BC为两个其余的边。根据勾股定理，得到以下的等式：
AC^2 + BC^2 = AB^2

这个定理可以用于求解直角三角形中的未知边长，或者判断一个三角形是否为直角三角形。例如，如果已知边AC的长度为3，边BC的长度为4，我们可以利用勾股定理求解边AB的长度。根据勾股定理的等式，我们有3^2 + 4^2 = AB^2，化简得到25 = AB^2，再求平方根得到AB的长度为5。因此，我们可以得出结论，在这个三角形中，边AB的长度为5，满足勾股定理的条件。

勾股定理的名字来源于西方古希腊的数学家毕达哥拉斯。尽管在中国古代数学中也有类似的定理，但是毕达哥拉斯定理的名字在世界范围内被广泛接受并使用。在中国，古代数学家商高也发现了这个定理的特例，将之称为商高定理。

勾股定理在数学和实际应用中都有重要的作用。它不仅可以用于解决直角三角形问题，还可以推广到其他几何形状和物理问题中。例如，勾股定理可以帮助我们计算三维空间中的距离、判断平面上的点是否位于同一直线上等等。在物理学中，勾股定理也被广泛应用于力学、电磁学等领域，用于描述物体运动的速度和加速度之间的关系。

勾股定理是数学中的一个重要定理，它描述了直角三角形中三边之间的关系。它的应用不仅限于几何学，还可以推广到其他学科中。无论是在数学课堂上还是在实际生活中，勾股定理都发挥着重要的作用。