勾股定理怎么计算-勾股定理计算公式

勾股定理是一个基本的几何定理，用于描述直角三角形的三条边之间的关系。根据勾股定理，直角三角形的斜边的平方等于两直角边平方和。即a²+b²=c²。这个定理的应用非常广泛，不仅可以用于计算三角形的边长，还可以用于判断一个三角形是否为直角三角形。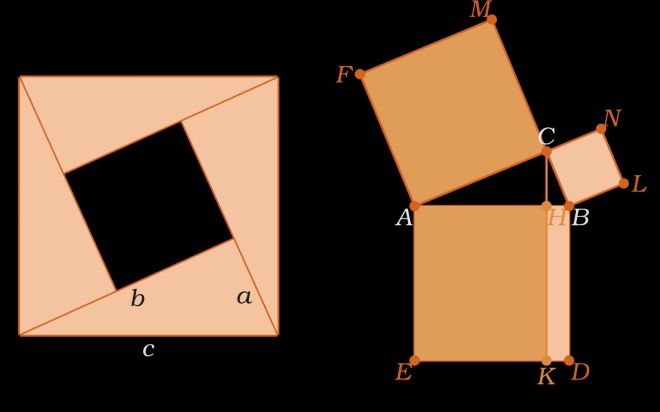

在计算中，如果已知直角三角形的两条直角边a和b的长度，我们可以通过勾股定理计算斜边c的长度。公式为c=√(a²+b²)。通过这个公式，我们可以快速准确地求得斜边的长度。

反之，如果已知斜边c的长度，可以通过勾股定理计算出直角三角形的其他两条边的长度。公式为a=√(c²-b²)或b=√(c²-a²)。这个定理不仅方便我们在实际问题中求解三角形的边长，同时也体现了数学之美，让我们能够更深入地理解直角三角形的内在关系。

此外，勾股定理还可以用于判断一个三角形是否为直角三角形。如果三角形的三条边长满足a²+b²=c²，那么这个三角形就是直角三角形。这样，我们可以通过简单的计算就可以判断一个三角形是否符合直角三角形的性质。

勾股定理不仅是一个重要的几何定理，更是一个实用的工具。通过勾股定理，我们可以更好地理解和解决直角三角形相关的问题，同时也能够在实际生活中运用这一定理，让我们的数学知识得到更广泛的应用。