勾股定理怎么算-勾股定理必背公式是什么

勾股定理是一个历史悠久且广为人知的几何定理，也是数学中最基本的定理之一。它描述了直角三角形中三条边之间的关系，给出了一个简单而精确的公式，帮助我们求解各种几何问题。

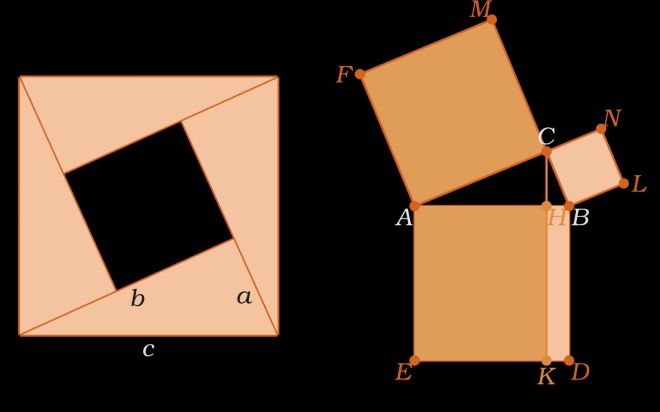
勾股定理的必背公式是：在任何一个直角三角形中，两条直角边的平方之和等于斜边的平方。这个公式可以用数学表达为：a² + b² = c²，其中a、b分别表示两条直角边的长度，c表示斜边的长度。

根据勾股定理的公式，我们可以解决各种与直角三角形相关的问题。比如，已知两条直角边的长度，我们可以通过求斜边的长度来完成三角形的计算。同样地，如果我们已知两条边和斜边的长度，我们也可以通过勾股定理来验证这是否为一个直角三角形。

勾股定理有许多不同的证明方法，据说已经有500种以上的证明方法。这些证明方法包括代数、几何、图形等多种思路，每一种方法都有其独特的思想和角度。这使得勾股定理成为了学习数学的一个重要的例子，通过掌握和理解这些证明方法，我们可以提高数学思维能力和解题技巧。

在求解问题时，我们还可以利用一些特殊的勾股数来简化计算和判断。勾股数是能够构成直角三角形的三边长度的三个正整数，例如3、4、5；6、8、10；5、12、13；7、24、25等。这些常见的勾股数可以帮助我们快速解决一些几何问题，提高解题的效率。

勾股定理是一个重要而实用的数学定理，它有着丰富的证明方法和应用场景。掌握勾股定理和相关知识，不仅可以帮助我们解决几何问题，还可以培养我们的数学思维和解题技巧。无论是在学校课堂还是在日常生活中，勾股定理都是我们不可或缺的数学工具之一。